AmitNv | Topologies | Nv neurons and nets

BEAM Robotics- based on Nervous Network Technology

This page lists various experiments with Nv circuits.

Nv Neuron

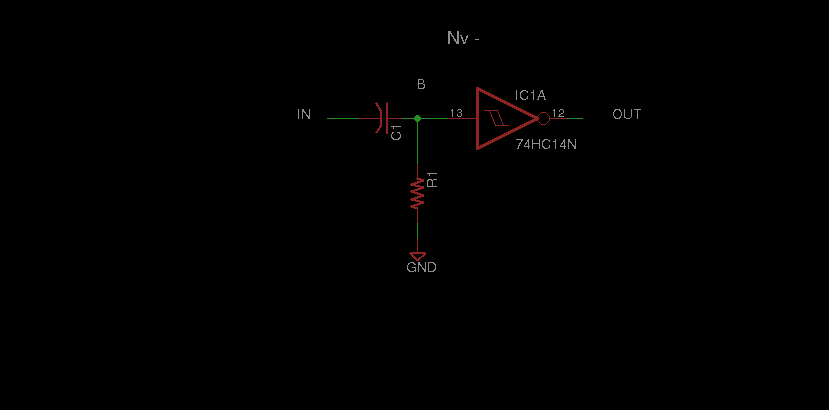
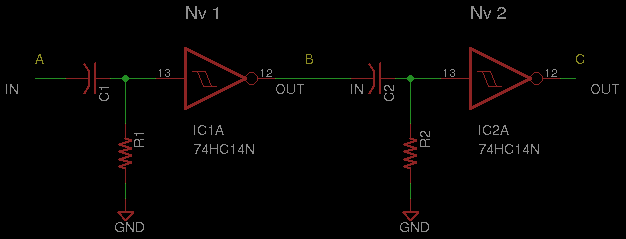
BEAM is based on nervous networks. The basic element of a nervous network is the neuron. BEAM tech makes use of several types of neuron, the most basic of which is the Nv motor neuron. It consists of an inverter, and an RC differentiator circuit. Specifically, a capacitive input and a resistor reference tied to either GND or VCC. The Nv responds to sudden changes at its input. This is due to the capacitor. The most common use of an Nv neuron is to delay the propagation of a signal. Also, the Nv uses negative logic, so an active neuron will have a output of 0v [low].

Click to open in new window

Nv Neuron	Waveforms

Click window to close

As it has an RC circuit, it has a time constant, T [tau]:

T = R x C | T in seconds | R in Ohms | C in Farads

There are 2 types of Nv neuron, a +ve Nv and a -ve Nv. This is based on if the resistor is tied to VCC or GND. I will not describe the circuit, as there are several
articles online worth reading.

You can read more about the Nv neuron at: Beam Wiki | Solarbotics Encyclobeamia | Wilf's Article [recommended] |

These neurons are usually interconnected in arrangements called nervous networks. There are several topologies used in constructing Nv networks. These are chains, branches and loops. Loops, and most non branched topologies are called n-cores, where n is a prefix denoting the number of neurons in the core. Bi, tri, quad, etc. Once upon a time, the quadcore, or microcore[old], was the most common topology, but now the bicore, or unicore[old] is the most commonly used controller. Pulses travel throught these networks, and are used to control various other actuatiors, circuits, etc. The Nv network can be said to be the brains of the bot, but it functions akin to the periphery nervous system of animals.

In addition to being delayed, the pulses traveling though the network can be augmented by the sensory data. This can generate signals which are sent to the actuators. This creates a feedback loop. Indeed, this shows the versatillity of the Nv controller for use in processing signals. This brings us to the next section, namely methods for influencing the pulses.

Parameterized Nv Neuron

The Nv neuron has several parameters which control it's pulse durations\:

Resistor Value [R]
Capacitor value [C]
Reference voltage [sign & magnitude]

By varying any one or any combination of these parameters, we can manipulate the Nv. Shown below is an Nv with circuitry for changing the resistor parameters. One circuit when activated will shorten the Nv pulse duration, while the other will lengthen it. In addition, the capacitor in the circuits [C2 & C3] will keep this parameter active for a period of time. It is also possible to influence the pulse duration of the Nv by using different capacitors at [C1] , but in general, the cost of a resistor remains the same regardless of the magnitude of resistance [cost inc with watts], whereas the cost of a capacitor increases with capacitance.

Resistor Parameterized Nv Neuron	Waveforms

From this basis, it is a very simple matter to input any form of sensor data into the Nv, causing it to alter it's pulse duration in response. We can either shorten or lengthen the pulse. An example of this would be in controlling a motor. A minimum of 2 Nvs are required to control a DC motor. Each Nv explicitly controls the motor's rotation in one direction. Now, in this standard configuration, the motor's output shaft will rotate by equal amounts if the T of the neurons are the same. What do we do if we wanted to turn the shaft more CCW, than CW? Simple. We can lengthen the pulse duration of the Nv responsible for CCW rotation. Or, we could shorten the pulse duration of the Nv responsible for Clock Wise roation. The latter is useful if the shaft has limits on its rotation. Also, both shcemes could be employed at once.

We have essentially parameterised the Nv, on the basis of resitance, for n resistors:
T = Ri x C ; { Ri | 1<= i <=n }

So, for any of the n resistors in use, we get a new T.
The first robot I know of to use a similar (less complex)scheme is Mark Tilden's Vbug 1.5 Walkman. The robot had 2 sensors for "crabwalking" laterally. The 5M2 walker in the robot's section uses both this original crabwalk scheme, and the shortening circuit to create a run function.

Argument Net

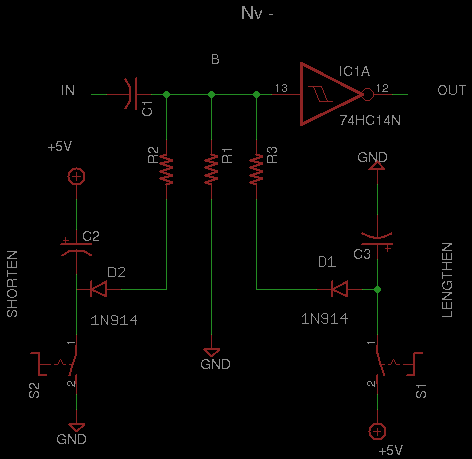
This is an offshoot of the Paramterized Neuron.
Above, it was shown how to parameterize an Nv neuron's resistor to change the its pulse duration. The same is done in this scheme, but there are some other elements.
In the first schematic, there is a chain of 4 Nvs. Each one is resistor parameterized. There are banks of resistors switched by a bilateral switch to ground. Each Nv has a parameterized resistor in these banks. So when the enable is set on the bilateral switch, all the Nv neurons in the chain will have altered pulse durations.
In addition, there is another set of resistors, individually switched by bilateral switches, but to +V. When one of these switches is thrown, the respective Nv changes from being an Nv- to an Nv+. This completely changes how the pulse will propogate in the network.

Now consider the 4 Nv chain, with each Nv having the same valued resistors and capacitors. The pulse durations will all be the same. When the pulse travels down the chain, the first Nv activates, then times out. The second activates then times out, and so on for the 3rd and 4th Nvs. The pulse travels at the same speed throughout the chain and each Nv. If we were to change the resistor parameter of one of the Nvs to be a smaller resistance, then this Nv would time out faster than the others, and the pulse would reach the proceeding neuron much more quickly than any of the others. The converse is true for larger resistances.
Effectively, in any network of n Nvs , the (n-1)th Nv acts as a timed delay, a "fuse" for the proceeding nth Nv "fire", ie:
the (n-i)th Nv delays the {n+(i+1)}th Nv, 1<= i <= n.

This is shown in the second schematic, where there is a 2 Nv chain, the first Nv is the fuse Nv, and the second is the fire Nv.

A-net Basic	A-net 1 Motor	A-net 2 Motors

Note that ANY neuron is the fuse for the proceeding neuron in the chain, in any network. So one does not explicitly need add in a single neuron to each of the firing ones, although, the a separate fuse neuron could be useful for processing sensory information for the fire neuron. This could be in the form of shortening or lengthening the fuse, ie, the pulse duration of the fuse neuron, via the scheme shown above. If the same shortening/lengthening of the pulse duration is applied to the fire, this would be able to asjust the pulse duration on the fly of the action.

Also shown on the second schematic are 2 asymmetrical bicores, one of each has a parameterized reference resistor connected to ground. The other reference resistor is tied to the A-net output. One of the bicore's outputs is labelled " PWM".
What this all means is that when the fire neuron activates, the bicore reference resistor tied to the A-net output will be grounded,hence the bicore activates,and will start to produce pulses at the PWM output.
These pulses, coupled with the standard A-net output are used to control a motor through a motor driver. The PWM varies the motor's speed, the A-net determines when the motor activates.

The most remarkable aspect about this scheme, is that by placing several A-net chains, soley in parallel, it would be possible to simulate/create ANY configuration of ANY core Nv network, simply by changing the resistance parameters.

To make a standard Nv chain of n neurons, n A-nets would be connected in parallel, such that the all receive the same input pulse. The resistors of each of the fuse neurons would each be sequentially of a higher resistance. So when the input pulse is supplied, the first A-net fuse times out, then the fire activates. The second A-net fuse would time out, causing the respective fire neuron to activate. This would continue to the nth A-net.
It would be possible to create loops in a similar manner as well, the nth A-net fire neuron's output would be connected to the collective inputs of the A-nets.

Nv Nets

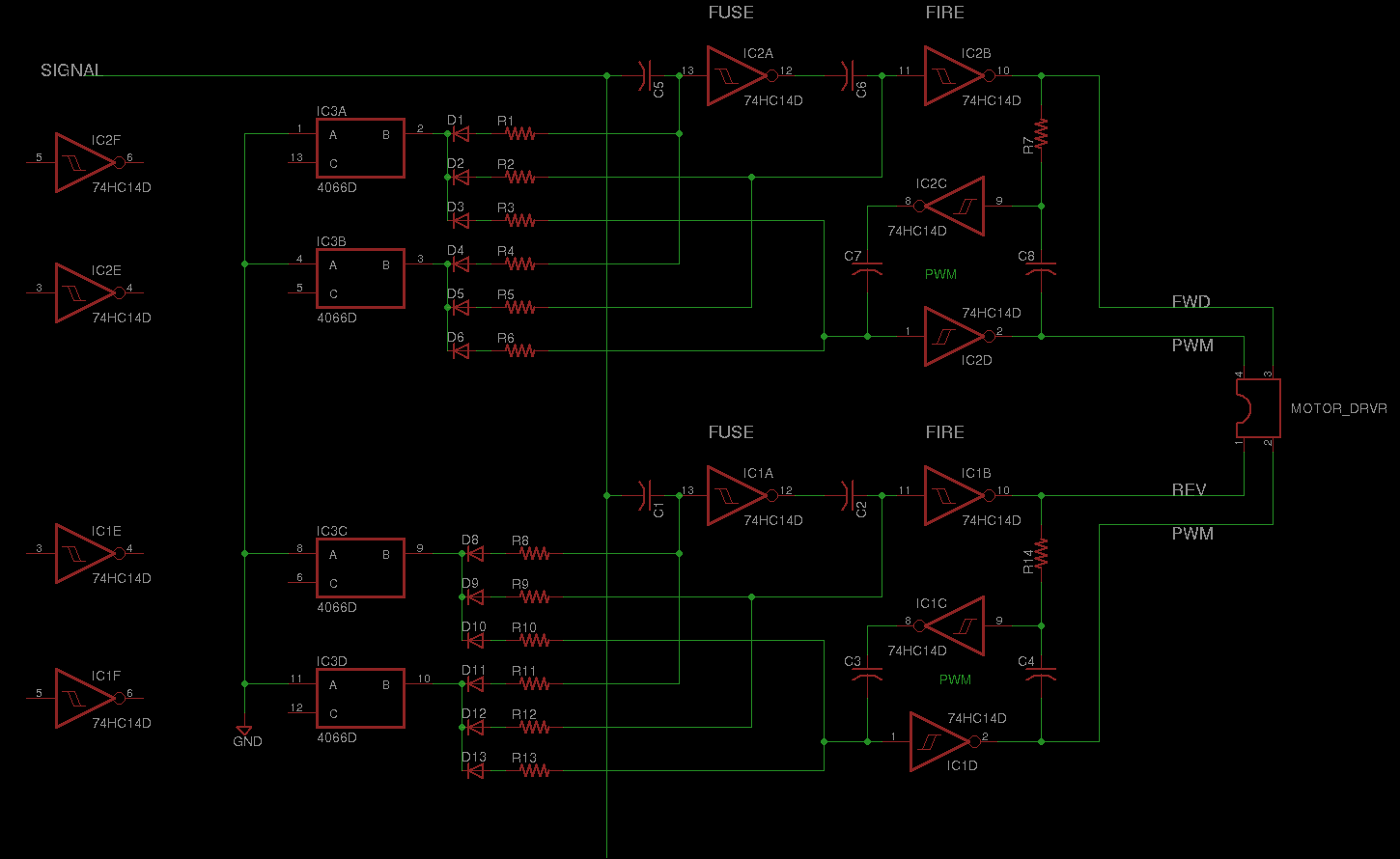
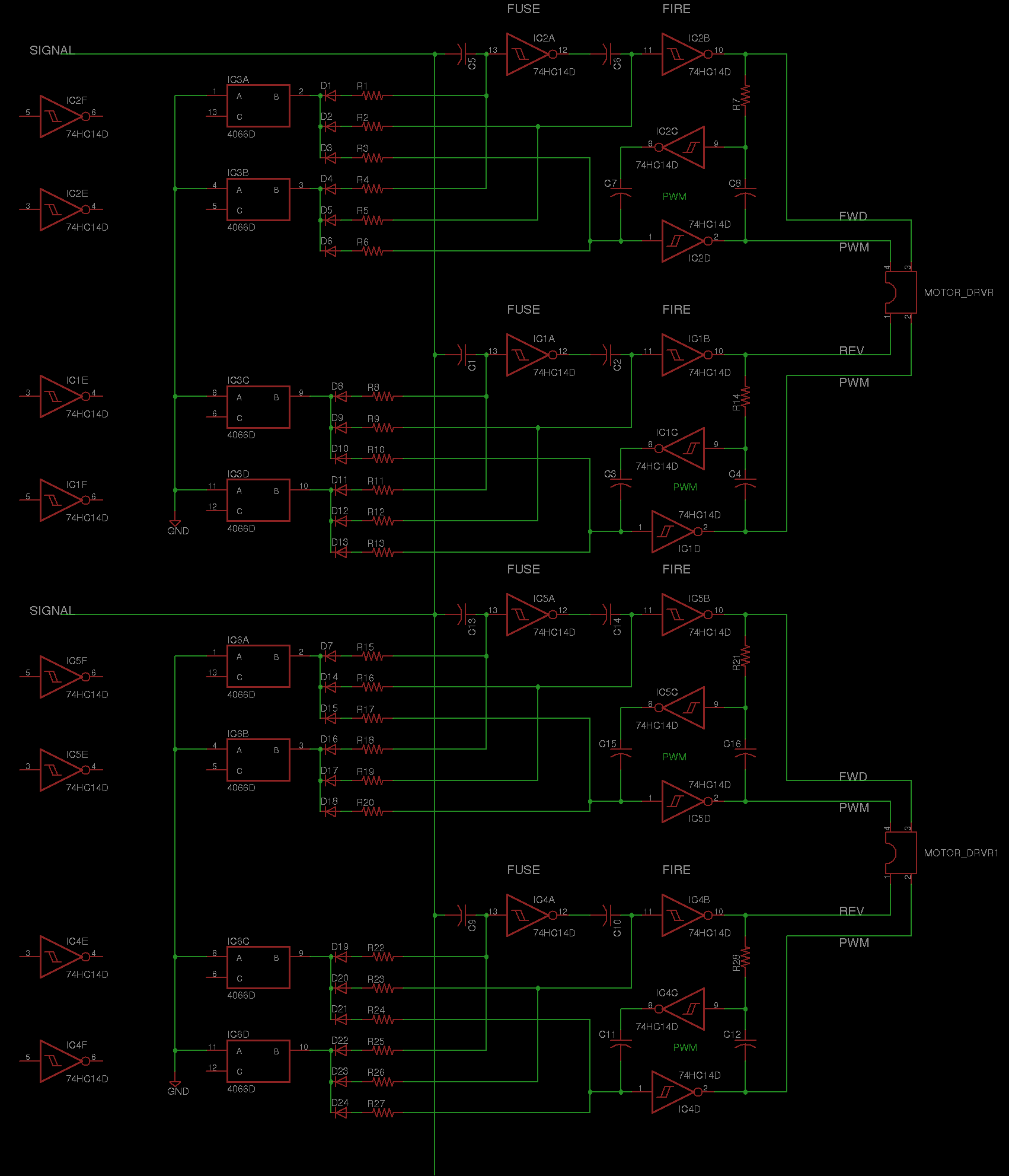
A single Nv neuron on it's own isn't too useful for the overall control of a robot. You could probably turn it into a standard schmitt oscillator then you could blink an LED for a beacon or sometihng. Indeed, Nvs are the most useful when they are connected in networks. The simplest network consists of 2 neurons, and it can only either be a chain or a loop. In addition, 2 neurons are the minimum nuber required to control a DC motor, as stated above.
Recall, the Nv- uses negative logic: 0V is ON & 5V is OFF.

2 Nv Network	Waveforms	4 Nv Loop	Waveforms

Click to open in new window			Click window to close

In a basic 2 Nv chain, such as the A-net above, the output of the first Nv is connected to the input of the second. Each of the resistors are referenced to ground.
If the input is originally at 0V, then the first Nv will be deactivated, it's output will be +5V. This means that the second Nv will have +5V at its input, hence it will activate, and produce an output of 0V.
A +5V square wave signal is supplied to the first Nv. As the input rises from 0 to 5 Volts, the first neuron will activate, so it's output will drop to 0V. This chane causes the second neuron's capacitor to discharge, resulting (after a delay)and after a delay, The second neuron will deactivate, so it's output will be 5V.
The input is lowered to 0V, the first neuron's capacitor will discharge, and the fist neuron will deactivate, its output will be +5V. This +5V at the second neuron's input will cause its capacitor to charge, eventually, the second neuron will activate, producing 0V at its output.
Remember that each of these occurences is time dependent, as explained in the first section.
T = R x C | T in seconds | R in Ohms | C in Farads

Each Nv in an Nv net generates a square wave of varying duty cycle.

Biomorphic maps are introduced. It would be much to cumbersome to repeteivly draw all the Nv circuitry over and over in a net, so a new set of symbols are used to represent the electronics involved.

Biomorphic Nv	Biomorphic Connections

Click to open in new window	Click window to close

The circuit diagram of the net will give you the assembly instructions. A Biomorphic Map of the Nervous Network is a graphical representation which shows how the Nervous Net functions .

You can see a full list of these symbols here: Biomorphic Maps | Nv & Nu Neurons | Symbols for Connecting Neurons |

State Diagrams are introduced. Much like the biomorphic map, In addition to showing the Nv neurons in the net, it shows the state of the neurons at a particular time, with either a 1'active' or a 0 'inactive'.

Gaits & Things

Nvs in my book are mainly motor neurons. Their use is to control motors, or actuators in general. The current Nv net designs floating around, have most if not all of their Nvs dedicated to the control of motors. It is possible to tailor an Nv net to produce a specific pattern, to move a set of motors in a specific way, ie you can build a net to precisely match a specific gait.

Click to open in new window

...	...

Click window to close

...

Hexapod

...

Click to open in new window

...	...

Click window to close

...